酸性度の計算

「酸性度」というと、色々な無機酸・有機酸の水中でのpKa値を想定される方が多いと思います。よく有機化学では、電子求引性置換基により酸性度が増強されるとか、共鳴構造が多く描けると酸性度が高いなどといった議論がされますが、これらは多くの場合水中でのpKa値を基にしていることと思います。しかし、このpKaという値が溶媒によって大きく変化することもよく知られています。これは、溶媒和に伴うエントロピー変化が酸解離平衡に重大な影響を及ぼしているためです。純粋な置換基効果の見積もりはpKaで行えないのです。

極力溶媒効果を排除した酸性度の指標として「気相酸性度(GA)」があります。これは文字通り気相中での酸性度で、IUPACの定義によると酸解離に伴うギブズエネルギー変化で表されます。酸解離に伴うエントロピー変化を排し、エンタルピー変化のみで表現したものは「プロトン親和力(PA)^※」と呼ばれ、置換基の電子的効果を比較するのに有用な指標となります。いずれも数多くの実験値も報告されており、文献によっては両者とも気相酸性度として報告しているケースもあります(例えばOrganic Chemistry InfoではPAをGAとして紹介しています)。ここでは、いくつかの有機分子の気相酸性度(GA及びPA)をPC GAMESSで計算して実験値と比較するとともに、MOPAC2007による計算(PA)で水中でのpKaとも比較してみたいと思います。

Carbon acid vs Oxygen acid

有機化合物で酸といえばカルボン酸が代表的ですが、その中でも酢酸は最も一般的な酸で、家庭で調味料として使う酢の一成分であり、合成化学では溶媒としても用いられます。水中でのpKaは4.76で、フェノールよりは強いが塩酸よりは弱い酸です。酢酸はカルボキシル基のO-Hが解離するので「酸素酸」に分類されます。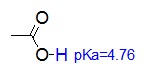
一方、C-Hが解離する酸を「炭素酸」と分類しますが、その多くは活性メチレン化合物で、メルドラム酸やアセト酢酸エステルが代表的です。ここでは最も原子数の少ない活性メチレン化合物としてマロノニトリルをターゲットにします。マロノニトリルはpKaが11.2で、エタノールよりは強いがフェノールよりは弱い酸です。
酢酸とマロノニトリルを比較すると、pKaの値を見れば一目瞭然、酢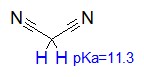酸のほうが100万倍以上強い酸です。しかし、プロトン親和力ΔH_acid⁰では酢酸が348.7±2.2 kcal/mol、マロノニトリルが335.8±2.1 kcal/molで、マロノニトリルの方が酸性度が高くなります(プロトン親和力は酸解離に必要なエンタルピーなので、小さい方が酸性度大)。計算化学では真空中が最も取り扱いやすく精度も高いので、真空により近い気相酸性度の予測を行ってみましょう。

酢酸もマロノニトリルも小分子ですので、モデリングの過程は省略します。それぞれ、中性分子と脱プロトン化したアニオンについて構造最適化と振動計算を行いますが、$CONTRLグループのRUNTYP=OPTIMIZEはそのままで、$STATPTグループにHSSEND=.T.を追加すると両方一度に行うことができます(Gaussianでいう「Opt Freq」に相当)。モデル化学としてRB3LYP/6-31+G(d,p)を、スケール因子は0.9717を用います(CCCBDBにあるマロノニトリルのZPEの実験値(9505.0 cm^-1)を再現するように設定しました)。

$CONTRL SCFTYP=RHF RUNTYP=OPTIMIZE COORD=UNIQUE
 MAXIT=200 NZVAR=15 ICHARG=0 MULT=1 DFTTYP=B3LYP $END
 $SYSTEM TIMLIM=600 MWORDS=1 AOINTS=DIST
 L2SIZE=1024 VOLSIZ=512 $END
 $STATPT NSTEP=500 OPTTOL=1.0E-05 METHOD=RFO HSSEND=.T. $END
 $FORCE SCLFAC=0.9717 $END
 $BASIS NGAUSS=6 GBASIS=N31 NDFUNC=1 NPFUNC=1 DIFFSP=.T. $END
 $SCF DIRSCF=.T. DAMP=.T. $END
 $ZMAT DLC=.T. AUTO=.T. $END
 $GUESS GUESS=HUCKEL $END
 $DATA
…(以下略)

計算結果の処理は、以下のように行います。まず、気相酸性度(ΔG_acid⁰, ΔH_acid⁰)の定義は、気相中298Kでの以下の反応のギブズエネルギー/エンタルピー変化です。

AH → A^– + H⁺

このうちH⁺のエンタルピー/エントロピーは、その定義より手計算で導くことができます。エンタルピーの定義は、

H = U + RT (1)

です。分子軌道計算では、内部エネルギーUは全電子エネルギーと並進・回転・振動エネルギーの和になります。

U = E_el + E_trans + E_rot + E_vib (2)

プロトンは電子を持ちませんので第1項は0、単原子なので第3項・第4項も0になります。よって、

U = E_trans = 3/2*RT (3)

となります。これを式(1)に代入して、T = 298.15 (K)より

H = 3/2*RT + RT = 5/2*RT = 1.4812 (kcal/mol)

と計算されます。
エントロピーも並進項のみになり、以下のように表されます。

S = S_trans = R[3/2*ln(2πm/h²) + 5/2*ln(kT) + ln(P) + 5/2] = 108.843 (cal/K·mol)

上式でmは分子質量(kg)，hはプランク定数，kはボルツマン定数，Pは圧力(Pa)です。
残りの2成分は、計算結果を基に計算を行います。PC GAMESSでは、全電子エネルギーはhartree，熱力学補正はkJ/mol及びkcal/mol単位で出力されますので、適宜変換定数(627.5095 kcal/mol/hartree)を使ってエンタルピーをkcal/mol単位で算出すると、以下のようになります。

AcOH

	H (kcal/mol)	G (kcal/mol)
AcOH	-143725.005	-143745.691
AcO–	-143380.512	-143400.685
H+	1.481	-6.275
Δ	345.974	338.731
exp.	348.7±2.2	341.7±2.0

 

CH₂(CN)₂

	H (kcal/mol)	G (kcal/mol)
CH2(CN)2	-141152.596	-141173.276
CH(CN)2–	-140823.749	-140844.133
H+	1.481	-6.275
Δ	330.328	322.867
exp.	335.8±2.1	328.1±2.0

実験値(出典: Fujio, M.; McIver, R.T., Jr.; Taft, R.W., J. Am. Chem. Soc., 1981, 103, 4017.)を概ね再現できているようです。

Acidity of alcohols

アルコールはアルキル置換が進むにつれてpKaが大きくなる(=酸性度が下がる)ということが知られています。実際、MeOH,EtOH,iPrOH,tBuOHはこの順にpKaが大きくなることが実験的に明らかになっています。しかし、この順序は気相中では逆転するということも、実験的に知られています。最新のMOPACであるMOPAC2007を使って、気相酸性度の序列を計算するとともに、PCM法でどれくらい水の溶媒効果が再現できるのかを見たいと思います。
こちらも先と同様、小分子ですのでモデリングは省略します。PCM計算では水の比誘電率として78.54を用い、Gradientが十分小さくならないうちに「HEAT OF FORMATION IS ESSENTIALLY STATIONARY」というメッセージとともに最適化が中断されることがあるので、一部「RECALC=2」をキーワードに加えています。エンタルピーとしては生成熱(H.O.F.)を用いますが、MOPACは298Kでの生成熱を基準としてエネルギーを計算しますので(ab initioでは0Kから積み上げる)、気相酸性度の値と計算値は大きくずれます。そのため、2軸折れ線グラフで値の変化傾向を比較することにします。MOPACの計算値はHOF(A-)-HOF(AH)です。

まずは、気相酸性度の比較。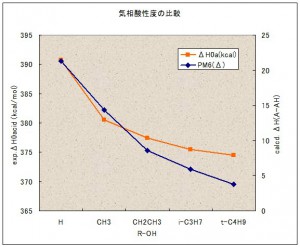
MOPACの計算値は、アルキル置換による酸性度の増強を再現しています。

 

 

 

 

続いて、pKaとPCM法で水和を考慮した計算値の比較。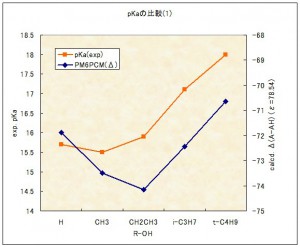

アルキル置換による酸性度の減弱を多少は再現できていますが、H2O,MeOHと他の3つのエネルギー的関係が再現できていません。が、水のような水素結合の要素が大きい溶媒でも、PCM法のような連続誘電体モデルである程度のモデル化が可能であることを示す結果でしょうか。更に再現性を上げるには、水分子をいくつか付着させて水素結合の要素を反映させた上でPCM法を行うことが考えられます。

 

ちなみに、MOPAC2007では酸素酸のpKaを予測することが可能になっています(キーワードPKA)。上記アルコールの例でやってみました。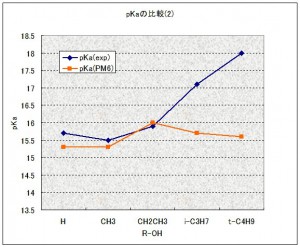

結果は見ての通り惨敗です。O-H結合長と電荷から計算しているようですが、その部分はアルコール同士で差がつかなかったということでしょうか…pKaの計算式を立てるのに用いた母集団は、もっと酸性度の高いフェノールやカルボン酸が中心ですので、致し方ない所かも知れません。

※PAの定義
プロトン親和力の正確な定義は、以下の反応の-ΔH⁰です。塩基の強さを議論するのに使いやすい名前・定義ですね。B = A^–と考えれば、酸解離の式と全く同一です。

B + H⁺ → [BH]⁺

[本稿で行った計算の入出力ファイル(1.4 MB) ]