分子間の相互作用は、計算化学が扱う主要な問題の一つです。単純に考えると、例えばAという分子とBという分子が相互作用してABという錯体を形成する場合、A,Bが単独で存在したときのエネルギーと錯体ABのエネルギーを比較して、その相互作用がどれぐらい強いかを議論するということになります。しかし、ここには思いがけない落とし穴が存在します。それが本稿で紹介するBSSE(Basis Set Superposition Error:基底関数重なり誤差)です。以下、GAMESSでのBSSEの計算方法とモデル化学による差について見てみたいと思います。
BSSEとは何か
先に述べた[A + B → A-B]における計算をもう少し詳しく見ると、Aを単独で計算するのと、A-Bという錯体で計算するのに違いがあることがわかります。即ち、錯体A-Bの中のAは、Bの基底関数を取り込むことができます。普通はこの「取り込み」はイコール相互作用ということになりますが、小規模の基底関数(例えばSTO-3Gや3-21Gなど)では、Bの基底関数をAの基底関数の分極関数やDiffuse関数のように使われてしまい、結果、相互作用のエネルギーだけでなく基底関数の改良による安定化エネルギーが取り込まれた形で数値が出ます。この「基底関数の改良による安定化エネルギー」こそがBSSEです。どんなに大規模な基底関数でもこの寄与が(大幅に縮小するとはいえ)完全に取り除けないことは、容易に想像できると思います。ですのでBSSEを求めることは、相互作用を扱う場合必須であると言えます。
(※これから紹介するBSSEの計算(counterpoise補償法)は、BSSEと完全にイコールではありません。よって、”BSSEを補正した”と言っても完全に除けたわけではなく、その比率が目的とする相互作用のエネルギーに比べて十分小さくするぐらいの意味合いで考えるべきでしょう。時には補正しすぎることもあるようです。)
BSSEの推定
メチルイソシアニド(CH3-NC)と三フッ化ホウ素(BF3)の錯体を例に、実際にBSSEを計算してみましょう。
本来、2分子間の相互作用はGibbs自由エネルギーで取り扱うべきですが、BSSEは全電子エネルギーに影響を与えるということと、計算時間の都合で振動計算は省略します(手抜きじゃないですよ?)。原系も生成系も対称性が高い構造をしていますので、メチルイソシアニドと錯体はC3vで、三フッ化ホウ素はD3hで計算を行うことにします。
それぞれの入力構造($DATAグループ)は以下のとおりです。非常に単純な分子なので、モデリングソフトを使うよりも手計算で組んだほうが早いでしょう。
$DATA (comment) Cnv 3 C 6.0 0.0000 0.0000 0.0000 N 7.0 0.0000 0.0000 1.1660 C 6.0 0.0000 0.0000 2.5900 H 1.0 1.0310 0.0000 2.9470 $END
$DATA (comment) Dnh 3 B 5.0 0.0000 0.0000 0.0000 F 9.0 1.3090 0.0000 0.0000 $END
$DATA (comment) Cnv 3 C 6.0 0.0000 0.0000 0.0000 N 7.0 0.0000 0.0000 1.1570 C 6.0 0.0000 0.0000 2.5750 H 1.0 1.0310 0.0000 2.9320 B 5.0 0.0000 0.0000 -1.7560 F 9.0 1.3300 0.0000 -2.0800 $END
これらについて、理論モデルとしてRHFとRPBE0(hybrid-DFT)を、基底関数として3-21Gと6-31G(d)を使い(つまり4種類の異なるモデル化学で)構造最適化を行ってみました。最適化のオプションとして、METHOD=RFO, OPTTOL=1.0E-05に設定しています($STATPT内)。それぞれ見積もられた相互作用エネルギーΔEは以下の通りです。
| Eel (kcal/mol) | |
| CH3-NC | -82303.62308 |
| BF3 | -201722.8716 |
| complex | -284046.4195 |
| ΔE | -19.92481976 |
|---|
| Eel (kcal/mol) | |
| CH3-NC | -82764.96653 |
| BF3 | -202808.2373 |
| complex | -285579.2782 |
| ΔE | -6.074389726 |
|---|
| Eel (kcal/mol) | |
| CH3-NC | -82718.39100 |
| BF3 | -202364.8063 |
| complex | -285109.6244 |
| ΔE | -26.42704571 |
|---|
| Eel (kcal/mol) | |
| CH3-NC | -83177.16892 |
| BF3 | -203461.1812 |
| complex | -286652.6213 |
| ΔE | -14.27117145 |
|---|
モデル化学によって、相互作用エネルギー(ΔE)の値は大きく異なります。3-21Gを使ったときに絶対値が大きくなる傾向にありますが、これはBSSEが多く含まれているためです。問題のBSSEですが、上記計算だけでは求められません。BoysのCounterpoise補償法では、あと4つエネルギー計算をする必要があります。
Counterpoise補償法では、「ゴースト原子」と呼ばれる「原子核がない、空の軌道だけがある原子」を利用してBSSEを見積もります(下図)。まず、最適化された錯体から一方のみをそっくり取り出し、単独でエネルギー計算(RUNTYP=ENERGY)を行います(E1)。次に、錯体の中で相手の方をゴースト化し、エネルギー計算を行い(E2)、両者の差を取ります(E1-E2)。つまり構造は全く同じで、相互作用する相手分子の軌道がある時とない時のエネルギー差が「BSSE」であるとするわけです。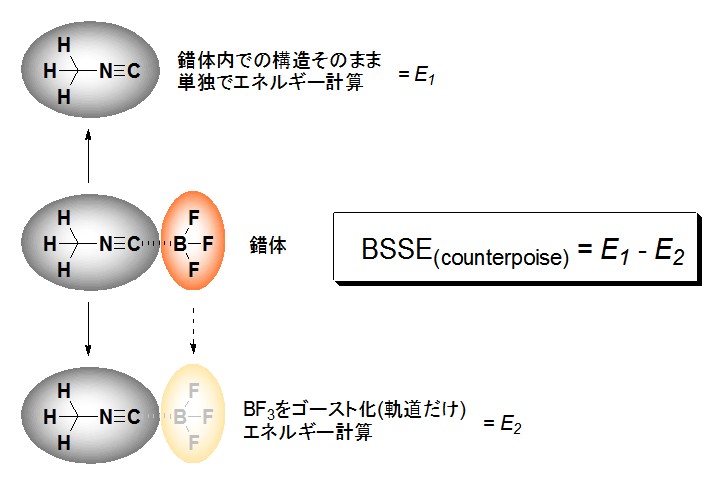
RPBE0/6-31G(d)を例に説明すると、まず、CH3-NC…BF3 complexの最適化構造を抜き出します。対称性は引き続き利用しますので、「COORDINATES OF SYMMETRY UNIQUE ATOMS」の方を使います。
C 6.0 0.0000000000 0.0000000000 -0.0011666630 N 7.0 0.0000000000 0.0000000000 1.1556337929 C 6.0 0.0000000000 0.0000000000 2.5688809713 H 1.0 1.0313791251 0.0000000000 2.9291276551 B 5.0 0.0000000000 0.0000000000 -1.7655824360 F 9.0 1.3279513381 0.0000000000 -2.0710495435
これをCH3-NCとBF3とに分けます。これら2つのエネルギー計算の和がE1の計算に相当します。
C 6.0 0.0000000000 0.0000000000 -0.0011666630 N 7.0 0.0000000000 0.0000000000 1.1556337929 C 6.0 0.0000000000 0.0000000000 2.5688809713 H 1.0 1.0313791251 0.0000000000 2.9291276551
B 5.0 0.0000000000 0.0000000000 -1.7655824360 F 9.0 1.3279513381 0.0000000000 -2.0710495435
次に、CH3-NCとBF3とをそれぞれゴースト化します。陽子数(2列目)を負の値にすればOKです。これら2つのエネルギー計算の和がE2の計算に相当します。
C 6.0 0.0000000000 0.0000000000 -0.0011666630 N 7.0 0.0000000000 0.0000000000 1.1556337929 C 6.0 0.0000000000 0.0000000000 2.5688809713 H 1.0 1.0313791251 0.0000000000 2.9291276551 B -5.0 0.0000000000 0.0000000000 -1.7655824360 F -9.0 1.3279513381 0.0000000000 -2.0710495435
C -6.0 0.0000000000 0.0000000000 -0.0011666630 N -7.0 0.0000000000 0.0000000000 1.1556337929 C -6.0 0.0000000000 0.0000000000 2.5688809713 H -1.0 1.0313791251 0.0000000000 2.9291276551 B 5.0 0.0000000000 0.0000000000 -1.7655824360 F 9.0 1.3279513381 0.0000000000 -2.0710495435
あとは、E1-E2でBSSE(counterpoise)が算出されます。前出の4つのモデル化学についてBSSEと補正ΔEを示します。(corr.ΔE = ΔE + BSSE : BSSE補正相互作用エネルギー)
| Eel (kcal/mol) | |
| ΔE | -19.92481976 |
| BSSE | 15.41135853 |
| corr.ΔE | -4.513461225 |
|---|
| Eel (kcal/mol) | |
| ΔE | -6.074389726 |
| BSSE | 4.158496483 |
| corr.ΔE | -1.915893243 |
|---|
| Eel (kcal/mol) | |
| ΔE | -26.42704571 |
| BSSE | 17.46429935 |
| corr.ΔE | -8.962746364 |
|---|
| Eel (kcal/mol) | |
| ΔE | -14.27117145 |
| BSSE | 5.530825435 |
| corr.ΔE | -8.740346015 |
|---|
3-21G基底を使った場合、BSSEが非常に大きくなっていることが一目瞭然です。6-31G(d)基底ではBSSEが大幅に減少しています。RPBE0ではBSSE補正がきちっと効いているのか、補正後のエネルギーが3-21Gと6-31G(d)でほとんど変わりません。比較のため、基底関数をさらに拡張した6-311+G(2d)と、6-31G(d)と同じスプリットバレンスDZ基底でDFTに最適化されているDZVP(6-41G(d)ぐらいに相当 : Can. J. Chem. 1992, 70, 560. EMSL Basis Set Exchangeから入手)でも同様に計算した結果を示します。
| Eel (kcal/mol) | |
| ΔE | -12.41652696 |
| BSSE | 0.932262563 |
| corr.ΔE | -11.4842644 |
|---|
| Eel (kcal/mol) | |
| ΔE | -14.86625195 |
| BSSE | 2.460337491 |
| corr.ΔE | -12.40591446 |
|---|
RPBE0/6-311+G(2d)の結果は流石に優れています。BSSEは1 kcal/mol以内。DZVPの結果も次いで良く、しかも6-311+G(2d)よりも3倍以上速く計算することができます。6-31G(d)とDZVPは所要時間はあまり変わらない(6-31G(d)が15.1 sec, DZVPが18.1 sec : ゴースト化錯体のエネルギー計算で比較)のですが、BSSEはDZVPが半分、最終的な補正エネルギーも6-311+G(2d)に近いということで、本系に対して非常に有効な基底関数のようです。
諸熊分割によるRHF法でのBSSE計算
RHF法に限り、上記のような複数の計算を行わなくてもCounterpoise補償法によるBSSEを計算することができます。最適化した錯体の構造を使い、$CONTRLグループでRUNTYP=MOROKUMAとし、$MOROKMグループに「BSSE=.T. IATM(1)=n」と記述します。また、対称性は利用せずにC1に、Direct SCFはできないので$SCFグループでDIRSCF=.F.にしています(デフォルトが.F.ですので、何も書かなくても構いません)。(下記例はRHF/3-21G)
$CONTRL SCFTYP=RHF RUNTYP=MOROKUMA COORD=UNIQUE MAXIT=200 NZVAR=0 ICHARG=0 MULT=1 $END $SYSTEM TIMLIM=600 MWORDS=1 AOINTS=DIST L2SIZE=1024 VOLSIZ=512 $END $BASIS NGAUSS=3 GBASIS=N21 $END $SCF DIRSCF=.F. DAMP=.T. $END $GUESS GUESS=HUCKEL $END $MOROKM BSSE=.T. IATM(1)=6 $END $DATA MeNC-BF3 complex, Morokuma decomp., RHF/3-21G C1 C 6.0 0.0000000000 0.0000000000 0.0092060324 N 7.0 0.0000000000 0.0000000000 1.1475972880 C 6.0 0.0000000000 0.0000000000 2.5926073449 H 1.0 -0.5112611246 0.8855302437 2.9363198310 H 1.0 -0.5112611246 -0.8855302437 2.9363198310 H 1.0 1.0225222492 0.0000000000 2.9363198310 B 5.0 0.0000000000 0.0000000000 -1.7648484631 F 9.0 -0.6662186811 1.1539246046 -2.0871738984 F 9.0 -0.6662186811 -1.1539246046 -2.0871738984 F 9.0 1.3324373622 0.0000000000 -2.0871738984 $END
IATM(1)=nの「n」は、モノマーの区切りを示すもので、上記のケースでは6番目までがメチルイソシアニドですので「6」としています。もし3成分以上の錯体だった場合は、各モノマーの最後の原子をカンマ区切りの番号で指定します(最後の1つは必要ありません)。
出力は一番最後で、以下のような内容です(抜粋)。
------------------------------------
RESULTS OF KITAURA-MOROKUMA ANALYSIS
------------------------------------
HARTREE KCAL/MOLE
ELECTROSTATIC ENERGY ES= -0.119363 -74.90
EXCHANGE REPULSION ENERGY EX= 0.154129 96.72
POLARIZATION ENERGY PL= -0.100479 -63.05
CHARGE TRANSFER ENERGY CT= -0.096449 -60.52
HIGH ORDER COUPLING ENERGY MIX= 0.094965 59.59
TOTAL INTERACTION ENERGY, DELTA-E= -0.067197 -42.17
DECOMPOSITION OF CT
CHARGE TRANSFER ENERGY, MON= 1 CT= -0.076927 -48.27
CHARGE TRANSFER ENERGY, MON= 2 CT= -0.019522 -12.25
DECOMPOSITION OF PL
EPL, MON= 1 PL= -0.083530 -52.42
EPL, MON= 2 PL= -0.010179 -6.39
HIGH ORDER COUPLING FOR PL, PMIX= -0.006769 -4.25
BASIS SET SUPERPOSITION ERROR
TOTAL INT WITH BSSE, DELTA-E(BSSE)= -0.042638 -26.76
BSSE CORRECTION, E(BSSE)= 0.024560 15.41
一番最後のBSSE CORRECTIONが目的の値です。先の手計算とも合致しています。
[本稿で行った計算の入出力ファイル(4.49MB)]
Leave a Reply
コメントを投稿するにはログインしてください。