NMR化学シフトの高速計算

分光学的に測定される分子のプロパティの中で、NMR(核磁気共鳴)スペクトルは有機化学者にとって最もなじみ深いものではないでしょうか。化合物の構造決定において、X線結晶構造解析、質量分析と並び極めて重要な位置を占めています。
量子化学計算プログラムの多くは、NMRの化学シフトやカップリング定数を計算することができます。ここでは、ORCA 4.1.0を使った計算例をご紹介します。

代表的な有機小分子での計算

一般的な化学シフトの範囲は¹Hで0～10 ppm, ¹³Cで0～220 ppmほどですので、その範囲をだいたい網羅するように9種類の有機小分子を選び、CDCl₃中での実測値をどれくらい再現できるか調べました。9種の有機分子と、基準となるTMS(Tetramethylsilane)の構造を以下に示します。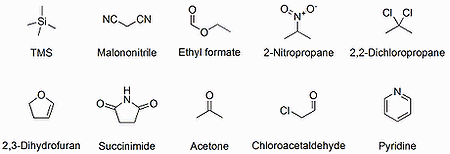

構造最適化はBP86-D3(BJ)/Def2-SV(P)で行い、PBE0/pcSseg-2でGIAO法による遮蔽定数の計算を行いました。溶媒効果はSMDモデルで考慮しました。代表的な入力ファイルの一例を以下に示します。

! Opt BP86 D3BJ Def2-SV(P) Def2/J RI PAL6
%cpcm
 smd true
 SMDsolvent "chloroform"
end
* gzmt 0 1
C
O 1 1.2
C 1 1.5 2 120
C 1 1.5 2 120 3 180
H 3 1.0 1 110 2 0
H 3 1.0 1 110 5 120
H 3 1.0 1 110 5 -120
H 4 1.0 1 110 2 0
H 4 1.0 1 110 8 120
H 4 1.0 1 110 8 -120
*

! PBE0 NMR TightSCF pcSseg-2 Autoaux RIJCOSX PAL6
%MaxCore 9000
%cpcm
 smd true
 SMDsolvent "chloroform"
end
* xyzfile 0 1 acetone_opt.xyz

結果を散布図にすると以下のようになります。

9mol_1H

9mol_13C

どちらの核種でも非常に良い相関関係ですが、計算値は若干数値を大きめに見積もる傾向があります(線形近似の傾きが１以上)。13Cでは一つ大きな外れ値がありますが、これは2,2-Dichloropropaneの2-Cで、ハロゲン原子が結合した炭素の化学シフトは過大評価する傾向があります。

大き目な分子での計算

より「現実的」なサイズの分子の例として、生理活性物質であるStrychnineとTriamcinolone Acetonideを取り上げます。これらを選んだ理由は、9つの小分子を選んだ時と同様に、ピークが広い化学シフトの範囲に散在しているためです。計算は先と同じモデル化学で実施しました。

Strychnine_1H

Strychnine_13C

Triamcinolone_1H

Triamcinolone_13C

こちらも非常に良い精度で計算ができています。ちなみに、Triamcinoloneの化学シフト計算は上記すべての計算で最も時間がかかりましたが、計算時間は筆者の環境で約3時間半でした。
ちなみに、今までの計算をすべて一つのグラフにまとめると以下のようになります。

All_1H

All_13C