有機化学の教科書で最初に出てくるエネルギープロファイル(反応座標とエネルギーを軸にとったグラフ)は、おそらくアルカンの回転障壁に伴うエネルギー変化だと思います。単結合まわりは、sp3軌道の軸対称の為に回転の自由度が高いですが、それでも回転に伴うエネルギー障壁(ねじれ歪みとも)は非常に重要で、配座を偏らせたり、立体障害が大きい場合には軸不斉のような現象を引き起こすこともあります。
ここでは、エタン(C2H6)とヒドラジン(N2H4)のC-CおよびN-N結合の回転障壁を、反応解析に於いて必須のテクニックであるポテンシャル面走査の手法・ミニマムエネルギーパス(Minimum Energy Path : MEP)計算によりMOPAC2007とPC GAMESSで計算した例を紹介します。
エタンの回転障壁
まず、エタンの回転障壁から。実験値はCCCBDBにある通り、凡そ12 kcal/molです。
最初にエタンをモデリングソフトで組みます。非常に単純な分子なので、手書きでz-matrixを組んでもいいでしょう。Winmostarで組んだMOPAC2007の入力ファイルの一例を示します。
PM6 EF PRECISE STEP=15 POINT=13 C2H6, rotation barrier C 0 0 0 0 0 0 0 0 0 C 1.4938 1 0 0 0 0 1 0 0 H 1.1 1 109 1 0 0 1 2 0 H 1.1 1 109 1 120 1 1 2 3 H 1.1 1 109 1 -120 1 1 2 3 H 1.1 1 109 1 0 -1 2 1 3 H 1.1 1 109 1 120 1 2 1 6 H 1.1 1 109 1 -120 1 2 1 6
z-matrixは、手書きで組んだ場合もこのようになることが多いでしょう。キーワードは、ハミルトニアンとして最新のPM6を用い、EF(Eigenvector Following)法で構造最適化を実施、計算精度を上げて(PRECISE:Energy Grad.の閾値を0.05に設定)います。ミニマムエネルギーパス計算の指定が「STEP=15 POINT=13」で、z-matrixの最適化フラグが「-1」に設定されている構造パラメータ(ここでは2面角)を、15度ずつ加算しながら13点(初期値含む)取って計算するという意味です。つまり、初期値の0度からスタートして、15度ずつ加算しながら13点、つまり180度まで計算するという意味です。
同じような意味で、以下のように入力を記述することもできます。
PM6 EF PRECISE C2H6, rotation barrier C 0 0 0 0 0 0 0 0 0 C 1.4938 1 0 0 0 0 1 0 0 H 1.1 1 109 1 0 0 1 2 0 H 1.1 1 109 1 120 1 1 2 3 H 1.1 1 109 1 -120 1 1 2 3 H 1.1 1 109 1 0 -1 2 1 3 H 1.1 1 109 1 120 1 2 1 6 H 1.1 1 109 1 -120 1 2 1 6 15 30 45 60 75 90 105 120 135 150 165 180
「STEP=x POINT=y」の代わりに、各点の構造パラメータ値を追加データとして記述しても、同じ計算ができます。両者に本質的な違いはありませんが、出力ファイルは違ってきます。STEP/POINTで記述した場合は、.arcファイルにエネルギー変化の要約のみが記述されますが、追加データで記述した場合は、.arcファイルに各点の最適化構造も出力されます。この.arcファイルはWinmostarで読み込んで連続的に表示することが可能ですので、計算された構造変化が意に沿った形になっているかを確認するには後者の方法が便利です。ここでは、エタンの回転という大きな構造変化を伴わないポテンシャル面の走査を行いますので、前者の方法で問題はないでしょう。
どのパラメータを変化させるか、というのは計算の成否に大きく関わります。上記のz-matrixでは、6番原子(水素)が「変化させたい二面角」で定義されていますので、これを「-1」とし、同じ炭素に結合している残り2つの水素(7番,8番)の2面角は6番原子で定義しています。これにより、6番水素原子の2面角を15度ずらすと他の2つの水素原子も15度ずれることになり、構造を変化させた直後の構造の歪みが最小限に抑えられます。
この計算は非常に速く、多くのPCで1秒以内には終了すると思います。出力ファイル(.out)の一番下に以下のような記述があり、これが2面角の変化に伴うエネルギー(生成熱,kcal/mol)の変化です。
POINTS ON REACTION PATH
AND CORRESPONDING HEATS
0.00 15.00 30.00 45.00 60.00 75.00 90.00 105.00
-14.86 -15.00 -15.35 -15.68 -15.82 -15.68 -15.35 -15.00
120.00 135.00 150.00 165.00 180.00
-14.86 -15.00 -15.35 -15.68 -15.82
PC GAMESSでの計算も、MOPAC2007の計算とほとんど変わりません。入力ファイルとしては以下のようなものを用意します。
$CONTRL SCFTYP=RHF RUNTYP=RSURFACE COORD=ZMT MAXIT=200 NZVAR=18 ICHARG=0 MULT=1 $END $SYSTEM TIMLIM=600 MWORDS=1 $END $STATPT NSTEP=500 OPTTOL=1.0E-05 IFREEZ(1)=12 $END $BASIS NGAUSS=3 GBASIS=STO $END $SCF DIRSCF=.F. DAMP=.T. $END $GUESS GUESS=HUCKEL $END $SURF NDISP1=7 DISP1=15 VECT1(12)=1 ORIG1=0 $END $DATA C2H6, rotation barrier C1 C C 1 1.4938 H 1 1.1 2 109 H 1 1.1 2 109 3 120 H 1 1.1 2 109 3 240 H 2 1.1 1 109 3 0 H 2 1.1 1 109 6 120 H 2 1.1 1 109 6 240 $END
まず、$CONTRLグループ内でRUNTYP=RSURFACEを指定します。RSURFACEとはRelaxed Surface Scanという意味で、各点で構造最適化しながらポテンシャル面を走査する方法です。COORD=ZMTとNZVAR=18でGaussian z-matrixを指定します。MOPAC z-matrixでも計算できますが、最適化フラグはPC GAMESSでは関係がないですので、すっきりした形のGaussian z-matrixを用いることが多いです。NZVARは構造パラメータの数で、一般に原子数×3-6です。
$STATPTグループ内ではIFREEZ(1)=12と指定します。これは12番目の構造パラメータを固定するという意味です。「12番目」とは、z-matrixの上から順に数えていって12番目という意味で、「1.4938」が1番目,「1.1」が2番目,「109」が3番目…と数えていって、12番目は6番原子(水素)の2面角「0」に当たります。
$SURFグループでMEP計算の設定をします。NDISP1=7はMOPACのPOINTに相当する値、DISP1=15はMOPACのSTEPに相当する値です。VECT(12)=1の説明は省略しますが、カッコ内の数字はIFREEZで指定した値、イコールの後ろは1にします。ORIG1=0は初期値で、0はz-matrixに入力された値(ここでは0)を初期値とすることを意味します。
本来はMOPACと同様にNDISP=13とするべきですが、PC GAMESSのz-matrix⇔cartesian座標変換に問題があり、途中で計算がうまくいかなくなるため、半分ずつ計算する必要があります(つまり、残り半分はz-matrixの0を90にするかORIG1=90にした入力ファイルで計算する)。
この計算はMOPACよりは時間がかかりますが、それでも10秒以内で終わることが多いでしょう。出力として参照すべきは、やはり.out(設定によっては.log)ファイルの末尾で、以下のような記述を探します。
OVERALL RESULTS OF THE RELAXED POTENTIAL SURFACE SCAN
------------------------------------
ICOORD1, |
COORD1 | ENERGY
---------------+--------------------
1 ( 0.00000)| -78.3016053819
2 ( 15.00000)| -78.3023120438
3 ( 30.00000)| -78.3039622967
4 ( 45.00000)| -78.3055431277
5 ( 60.00000)| -78.3061796409
6 ( 75.00000)| -78.3055434370
7 ( 90.00000)| -78.3039629172
ENERGY DELTA MAP(S) (W.R. TO THE LOWEST FOUND)
------------------------------------
ICOORD1, | ENERGY
COORD1 | DELTA
---------------+--------------------
1 ( 0.00000)| 0.0045742591
2 ( 15.00000)| 0.0038675972
3 ( 30.00000)| 0.0022173443
4 ( 45.00000)| 0.0006365132
5 ( 60.00000)| 0.0000000000
6 ( 75.00000)| 0.0006362040
7 ( 90.00000)| 0.0022167237
... DONE WITH RELAXED POTENTIAL SURFACE SCAN ...
上のテーブルは、各点での全電子エネルギーをhartree単位で出力したものです。下のテーブルは、テーブル内で最もエネルギーの低かった点を0とした相対値(こちらもhartree単位)で出力したものです。通常は下のテーブルを使うのが便利ですが、MEP計算を90度のところで半分に分けているため、90度より先にもっと低エネルギーの点があるかもしれませんので、上のテーブルを使うことにします。
残り半分の計算結果とつなぎ合わせると以下のようになります。
------------------------------------
ICOORD1, |
COORD1 | ENERGY
---------------+--------------------
1 ( 0.00000)| -78.3016053819
2 ( 15.00000)| -78.3023120438
3 ( 30.00000)| -78.3039622967
4 ( 45.00000)| -78.3055431277
5 ( 60.00000)| -78.3061796409
6 ( 75.00000)| -78.3055434370
7 ( 90.00000)| -78.3039629172
1 ( 0.00000)| -78.3039629172
2 ( 15.00000)| -78.3023120638
3 ( 30.00000)| -78.3016053818
4 ( 45.00000)| -78.3023126730
5 ( 60.00000)| -78.3039654649
6 ( 75.00000)| -78.3055453275
7 ( 90.00000)| -78.3061796409
上半分の一番下と、下半分の一番上は同じ90度の値ですので、エネルギー値も一致しています。このテーブルを使ってグラフ化を行います。
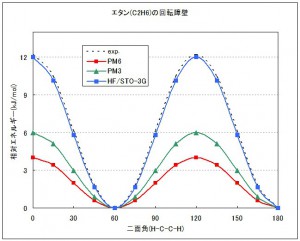
実際にグラフ化したものをFig.1に示します。
MOPACによる計算では、PM6,PM3どちらも実測値より大幅に低く見積もられいるのに対し、PC GAMESSによるab initio計算では、最も近似レベルの低いRHF/STO-3Gでも十分実験値を再現できていることがわかります。半経験的手法であるMOPACでは、MNDO法以降にNDDO近似(ある電子の2原子間にわたる微分重なりを0とする)が導入されており、これは2電子反発積分と重なり積分の無視を意味します。これが原因で、MOPAC(MNDO,AM1,PM3,PM5,RM1,PM6)ではこのような回転障壁を過小評価し、ab initio法ではそのような近似は入らないため、よく実験値を再現できたと考えられます。
ヒドラジンの回転障壁
エタンと電子的に等価なヒドラジンですが、そのN-N結合に対するポテンシャル変化はエタンのそれと大きく異なります。実験値はCCCBDBによると、H-N-N-Hが0度のとき36 kJ/mol、90度が最安定で、180度のとき13 kJ/mol程度です。今度はab initio計算での検討を中心にします。とはいえ、まずはMOPAC2007でPM6による計算を行ってみましょう。入力ファイルの1例を以下に示します。
PM6 EF PRECISE STEP=10 POINT=19 N2H4, rotation barrier N 0 0 0 0 0 0 0 0 0 H 1.1 1 0 0 0 0 1 0 0 H 0.997418 1 106.7271 1 0 0 1 2 0 N 1.455 1 106.7242 1 116.1228 1 1 2 3 H 0.997286 1 106.7242 1 0 -1 4 1 2 H 0.997418 1 108.7239 1 114.7817 1 4 5 1
エタンの時よりも細かく点を取っています。他は特に変わりません。計算時間はやはり1秒以内におさまると思います。結果の出力もエタンと同様です(下記)。
POINTS ON REACTION PATH
AND CORRESPONDING HEATS
0.00 10.00 20.00 30.00 40.00 50.00 60.00 70.00
26.43 26.19 25.55 24.63 23.56 22.47 21.43 20.51
80.00 90.00 100.00 110.00 120.00 130.00 140.00 150.00
19.72 19.05 18.48 17.95 17.44 16.93 16.42 15.95
160.00 170.00 180.00
15.57 15.31 15.22
PC GAMESSでの計算も、エタンの場合と変わりません。例えば以下のようになります。
$CONTRL SCFTYP=RHF RUNTYP=RSURFACE COORD=ZMT MAXIT=200 NZVAR=12 ICHARG=0 MULT=1 $END $SYSTEM TIMLIM=600 MWORDS=1 $END $STATPT NSTEP=500 OPTTOL=1.0E-05 IFREEZ(1)=9 $END $BASIS NGAUSS=3 GBASIS=STO $END $SCF DIRSCF=.F. DAMP=.T. $END $GUESS GUESS=HUCKEL $END $SURF NDISP1=10 DISP1=10 VECT1(9)=1 ORIG1=0 $END $DATA N2H4, rotation barrier C1 N N 1 1.4460 H 1 1.0160 2 108.85 H 1 1.0160 2 108.85 3 120.00 H 2 1.0160 1 108.85 4 0.00 H 2 1.0160 1 108.85 5 120.00 $END
計算時間もエタンとほぼ同じくらいです。2回に分けた計算結果をつなぎ合わせると以下のようになります。
------------------------------------
ICOORD1, |
COORD1 | ENERGY
---------------+--------------------
1 ( 0.00000)| -109.7338934764
2 ( 10.00000)| -109.7345223571
3 ( 20.00000)| -109.7362357138
4 ( 30.00000)| -109.7386211587
5 ( 40.00000)| -109.7412172564
6 ( 50.00000)| -109.7436351982
7 ( 60.00000)| -109.7456081011
8 ( 70.00000)| -109.7469994285
9 ( 80.00000)| -109.7477890609
10 ( 90.00000)| -109.7480536940
1 ( 0.00000)| -109.7480536941
2 ( 10.00000)| -109.7479537838
3 ( 20.00000)| -109.7477201855
4 ( 30.00000)| -109.7476099124
5 ( 40.00000)| -109.7478118710
6 ( 50.00000)| -109.7483554583
7 ( 60.00000)| -109.7491066437
8 ( 70.00000)| -109.7498502311
9 ( 80.00000)| -109.7503845392
10 ( 90.00000)| -109.7505775275
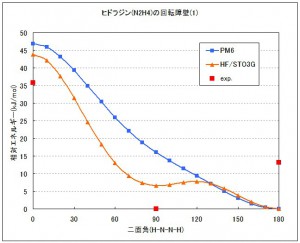
グラフ化した結果はFig.2 の通りです。実測値は連続値ではないので点で示しますが、明らかに合っていません。HF/STO-3Gでは90度に極小値がありますが、最小値ではありません。この結果から、ヒドラジンの回転障壁を再現するには、より進んだ理論モデルを用いる必要があると考えられます。
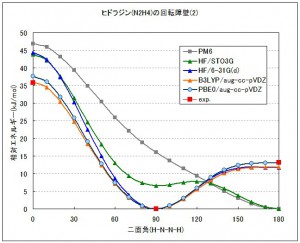
最終的に密度汎関数理論(DFT)の導入と、電子相関用にデザインされたDunningのcorrelation consistent基底を利用することによって、実験値とよく合致するポテンシャル曲線を得ることができました(Fig.3)。DFTの汎関数として2つのhybrid汎関数(B3LYP,PBE0)を用いましたが、どちらも非常に良い結果を与えています。
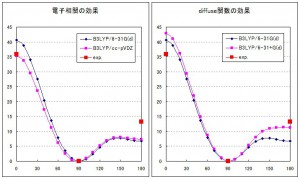
ちなみに、0度周辺のポテンシャルは基底関数自体の質(電子相関を考慮するのに適しているかどうか)で精度が決まり、180度周辺のポテンシャルはdiffuse関数(核から離れた領域に広がる電子を記述する関数)の有無で精度が決まるようです(Fig.4)。
[本稿で行った計算の入出力ファイル(2.44 MB)]
Leave a Reply
コメントを投稿するにはログインしてください。