分子には基底状態と励起状態があります。多くの有機反応は基底状態で起こりますが、光照射下では励起状態からも反応が起こります。また、紫外・可視スペクトルは共役系の状態を知るために有用な情報を与えますが、これは電子の励起エネルギーを観測していることに他なりません。当然、物質の色もこの電子励起に伴う光吸収に起因しています。
励起状態は、分子軌道計算でもちろん扱うことができます。ですが、励起状態は基底状態と異なり無数にあるので、その取り扱いは時に非常に難しくなります。ここでは、最もよく励起状態が調べられている分子の一つ・ホルムアルデヒドを例に、励起エネルギーの計算と励起状態の構造最適化について概観します。
励起状態の計算を始める前に
ホルムアルデヒドの電子励起のうち最も低いエネルギーで起こるのはn-π*遷移です。この垂直遷移のエネルギーは4.1または4.2 eVと実験的に求められています(JPC, 1981, 75, 2952.)。この値は、分子軌道計算でどこまで再現されるでしょうか。
ホルムアルデヒドの基底状態の構造も実験的に求められているので(Gurvich, L.V.; Veyts, I. V.; Alcock, C. B., Thermodynamic Properties of Individual Substances, Fouth Edition, Hemisphere Pub. Co., New York, 1989 : CCCBDBより引用 )、計算にはこれを利用します。非常に単純な分子なので、構造データを元に自分でz-matrixを組んだほうが早いでしょう。GAMESSの$DATAグループにGaussian Z-matrix形式で記述すると、例えば以下のようになります。
$DATA comment Cnv 2 O C 1 1.205 H 2 1.111 1 121.90 H 2 1.111 1 121.90 3 180.00 $END
励起状態を計算するには、分子の軌道がどのようになっているかを前もって知っておく必要があります。そこで、まずは上記の構造でRHFによる1点計算(MOPACでいう1SCF, GAMESSならRUNTYP=ENERGY)を行い、軌道の対称性を予め調べます。
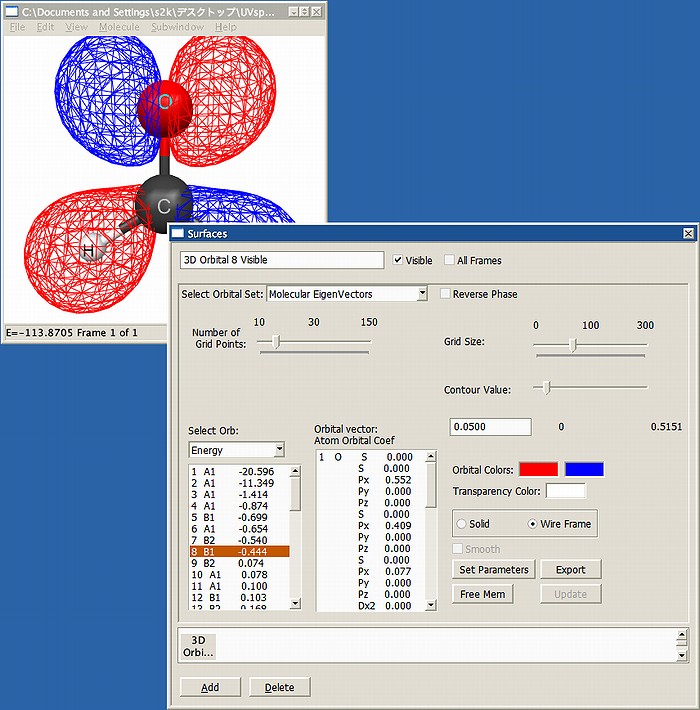
例として、PC GAMESSでRHF/6-31+G(d)の1点計算を実施し、MacMolPltで軌道を調べているところをFig.1に示します。C2v対称を指定して計算したため、軌道の対称性としてはA1,A2,B1,B2の対称種(既約表現)のみが出てきます。酸素原子のlone pairは8番目の軌道でB1、また励起先のπ*軌道は9番目の軌道でB2であることがわかります。励起状態の対称種は、半占軌道の対称種の掛け算になりますので、C2vの直積表よりA2となります。
※直積表をはじめ群論の各種データは群論のホームページに詳しいです。
さて、ここまでで準備は完了です。PC GAMESSでは励起状態の計算法として主にCIS, TDDFT, MRMP2を、WinGAMESSでは更にEOM-CCSDも利用できます。本稿では以下CIS, TDDFT, EOM-CCSDについて紹介します(MRMP2はCASSCFとともに別の記事にする予定です)。
CIS (Configuration interaction Singles)
CISはab initio計算で励起エネルギーを見積もる際、最も計算コストの低い方法といえます。PC GAMESSでの入力は、例えば以下のようになります。
$CONTRL SCFTYP=RHF RUNTYP=ENERGY COORD=ZMT CITYP=CIS MAXIT=200 NZVAR=6 ICHARG=0 MULT=1 $END $SYSTEM TIMLIM=600 MWORDS=1 $END $BASIS NGAUSS=6 GBASIS=N31 NDFUNC=1 DIFFSP=.T. $END $SCF DIRSCF=.T. DAMP=.T. $END $GUESS GUESS=HUCKEL $END $CIS NSTATE=1 $END $DATA HCHO, energy, CIS/6-31+G(d) Cnv 2 O C 1 1.205 H 2 1.111 1 121.90 H 2 1.111 1 121.90 3 180.00 $END
重要なのは$CONTRLグループでCITYP=CISを指定し、$CISグループでいくつの励起状態を解くか(NSTATE=n)を指定します。この例では、最低励起状態1つを解くように指定しています。この計算はかなり速く、筆者のPCでは0.9秒(2 CPU)で終了しました。出力の中で特に重要なところを抜粋したものを、以下に示します。
EXCITED STATE 1 ENERGY= -113.7005051917 S = 0.0 SPACE SYM = A2
----------------------------------------------
SINGLE EXCITATION SAP COEFFICENT
FROM MO TO MO
----------------------------------------------
5 9 0.08238576
5 13 0.07496784
5 17 0.05483138
8 9 0.74127528
8 13 0.62194065
8 17 0.19453207
8 21 -0.06806042
8 28 0.05817873
----------------------------------------------
------------------------------------------------------------------------------
CI-SINGLES EXCITATION ENERGIES
STATE HARTREE EV KCAL/MOL CM-1 NANOMETERS OSC. STR.
------------------------------------------------------------------------------
1A2 0.1693505391 4.6083 106.2691 37168.15 269.05 0.0000000
上の方の表は、その励起状態の中身を示していて、どの軌道からどの軌道へ励起した状態がどれぐらいの寄与をしているかがまとめれらています。下の方の表は励起エネルギーをまとめたもので、いろいろな単位で書かれています。よく使うのはEV(電子ボルト, eV)とNANOMETERS(波長, nm)でしょうか。右端のOSC. STR.は振動子強度で、吸収強度と相関しています。n-π*遷移は禁制遷移なので振動子強度は0です。STATEが先に調べたとおり1A2なのも確認してください。
TDDFT (Time-dependent DFT)
TDDFTはDFTにおけるCISのような理論で、入出力も似通っています。DFTは原理的に電子相関をある程度含んでいますので、CISよりも計算精度が期待できます。PC GAMESSでの入力例は以下の通りです。
$CONTRL SCFTYP=RHF RUNTYP=ENERGY COORD=ZMT CITYP=TDDFT MAXIT=200 NZVAR=0 ICHARG=0 MULT=1 DFTTYP=B3LYP $END $SYSTEM TIMLIM=600 MWORDS=1 $END $BASIS NGAUSS=6 GBASIS=N31 NDFUNC=1 DIFFSP=.T. $END $SCF DIRSCF=.T. DAMP=.T. $END $GUESS GUESS=HUCKEL $END $TDDFT NSTATE=1 ISTSYM=2 $END $DATA HCHO, energy, TD-B3LYP/6-31+G(d) Cnv 2 O C 1 1.205 H 2 1.111 1 121.90 H 2 1.111 1 121.90 3 180.00 $END
重要なのは$CONTRLグループでCITYP=TDDFTを指定し、$TDDFTグループでいくつの励起状態を解くか(NSTATE=n)とどの対称性を解くか(ISTSYM=n)を指定します。この例では、1A2の最低励起状態1つを解くように指定しています。この計算もかなり速く、筆者のPCでは3.3秒(2 CPU)で終了しました。出力の中で特に重要なところを抜粋したものを、以下に示します。
EXCITED STATE 1 ENERGY= -114.3613133261 S = 0.0 SPACE SYM = A2
----------------------------------------------
EXCITATIONS & DEEXCITATIONS SAP COEFFICENT
FROM MO TO MO
----------------------------------------------
8 9 0.99702864
9 8 -0.03267131
8 13 -0.07017684
13 8 0.00490047
----------------------------------------------
------------------------------------------------------------------------------
TDDFT EXCITATION ENERGIES
STATE HARTREE EV KCAL/MOL CM-1 NANOMETERS OSC. STR.
------------------------------------------------------------------------------
1A2 0.1474950440 4.0135 92.5546 32371.42 308.91 0.0000000
CISと全く同じフォーマットで出力されます。
EOM-CCSD (Equation of motion CCSD)
EOM-CCSDは高精度な電子状態理論である結合クラスター理論(Coupled Cluster, 略してCC)を励起状態に導入したもので、理論的にはGaussianに組み込まれているSAC-CIと等価とされています。PC GAMESSにはCCが含まれていないため計算できませんが、WinGAMESSで計算が可能です。WinGAMESSでの入力例は以下の通りです。
$CONTRL SCFTYP=RHF RUNTYP=ENERGY COORD=ZMT CCTYP=EOM-CCSD MAXIT=200 NZVAR=0 ICHARG=0 MULT=1 $END $SYSTEM TIMLIM=600 MWORDS=10 $END $BASIS NGAUSS=6 GBASIS=N31 NDFUNC=1 DIFFSP=.T. $END $SCF DIRSCF=.T. DAMP=.T. $END $GUESS GUESS=HUCKEL $END $EOMINP GROUP=C2V NSTATE(1)=0,1,0,0 IROOT(1)=2,1 $END $DATA HCHO, energy, EOM-CCSD/6-31+G(d) Cnv 2 O C 1 1.205 H 2 1.111 1 121.90 H 2 1.111 1 121.90 3 180.00
重要なのは$CONTRLグループでCCTYP=EOM-CCSDを指定し、$EOMINPグループで対称性(GROUP=xxx),どの対称性の励起状態をいくつ解くか(NSTATE(1)=n,n,n,n)などを指定します。NSTATE(1)の後は対称性に依存し、C2vではA1,A2,B1,B2の順になります(なので、上記の例ではA2を1状態という意味で0,1,0,0と書いています)。この計算はちょっと時間がかかり、筆者のPCでは15.5秒(1 CPU)で終了しました。出力の中で特に重要なところを抜粋したものを、以下に示します。
SYMMETRY OF THE STATE: A2
THE LARGEST R1 AND R2 AMPLITUDES FOR THIS ROOT ARE
R1= 0.0649149228 FOR I -> A = 5 9
R1= 0.4987975139 FOR I -> A = 8 9
R1= -0.0627353439 FOR I -> A = 5 13
R1= -0.4396541396 FOR I -> A = 8 13
R1= 0.0928135363 FOR I -> A = 8 17
R1= 0.0602705558 FOR I -> A = 8 21
R2= 0.0574399264 FOR I,J -> A,B = 8 7 13 13
R2= 0.0574399264 FOR I,J -> A,B = 7 8 13 13
GROUND STATE'S WEIGHT R0 = 0.0000000000
REL DIAGNOSTIC (R1*R1 + 2*R2*R2): 1.073
THE TOTAL ENERGY OF ROOT 1 IS E(EOM-CCSD) = -114.0401002850
---- SUMMARY OF EOM-CCSD CALCULATIONS ----
EXCITATION EXCITATION TOTAL
SYMMETRY ENERGY (H) ENERGY (EV) ENERGY (H) ITERATIONS
A2 0.14903242 4.055 -114.04010028 CONVERGED
見た目は違いますが、書かれていることはCISやTDDFTのときと何ら変わりません。CCSDなので、2電子励起配置も考慮に入っています(R2の行)。
まとめ
さて、いくつかの手法を用いてホルムアルデヒドのn-π*遷移エネルギーの計算をしました。Winmostarに同梱のCNDO/Sで計算した結果と合わせて以下に示します。
| ΔE(n-π*) (eV) | |
|---|---|
| exp. | 4.1, 4.2 |
| CIS/6-31G+(d) | 4.6083 |
| TD-B3LYP/6-31+G(d) | 4.0135 |
| EOM-CCSD/6-31+G(d) | 4.055 |
| CNDO/S(西本-又賀式) | 3.319 |
CISはやや過大評価,CNDO/Sは過小評価していますが、電子相関がよく考慮された後の2つはいずれも実験値に近い値になっています。励起エネルギーの評価に電子相関が重要であることがわかります。ちなみに、CISは定量性は見ての通りあまり期待できませんが、定性的にはよい一致を見せることが多く、計算速度の速さもあって簡単な見積もりには有用な方法のようです。
励起状態の構造最適化
垂直遷移のエネルギーを求める分には基底状態の構造で計算が行えますが、当然励起状態には基底状態とは異なる最安定構造が存在するはずです。GAMESSではCISとMCSCFで励起状態の構造最適化が行えますが、ここではCISの手順のみ示します(MCSCFについては、MRMP2による励起エネルギー計算と合わせて別記事を作成予定です)。
まず最初に、基底状態の構造を初期構造として、励起一重項状態の構造最適化を試みてみます。入力ファイルの基本は先の励起エネルギー計算の入力と同じで、$CONTRLグループのRUNTYPをOPTIMIZEに変更するだけです。それにプラスして、最適化後の構造が正しく最適化されているかをチェックする意味で、$STATPTグループにHSSEND=.T.を追加し、振動解析を最後に実行するようにしています。
$CONTRL SCFTYP=RHF RUNTYP=OPTIMIZE COORD=ZMT CITYP=CIS MAXIT=200 NZVAR=6 ICHARG=0 MULT=1 $END $SYSTEM TIMLIM=600 MWORDS=1 $END $BASIS NGAUSS=6 GBASIS=N31 NDFUNC=1 DIFFSP=.T. $END $SCF DIRSCF=.T. DAMP=.T. $END $GUESS GUESS=HUCKEL $END $CIS NSTATE=1 $END $STATPT HSSEND=.T. $END $DATA HCHO, S1 state geometry optimization, CIS/6-31+G(d) Cnv 2 O C 1 1.205 H 2 1.111 1 121.90 H 2 1.111 1 121.90 3 180.00 $END
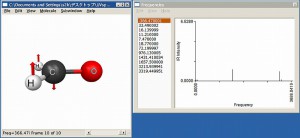
計算を実行すると、振動計算から興味深いことがわかります。Fig.2に可視化した画面を示しますが、得られた構造は1つの虚振動を有し、これは平面性を崩す方向の振動です。つまり、真の構造はピラミッド型であることを示唆しています。ということは、対称性の縛りを緩めて初期構造もピラミッド型にしておけば速やかに最適化できると考えられますので、以下のように入力を修正します。
$CONTRL SCFTYP=RHF RUNTYP=OPTIMIZE COORD=ZMT CITYP=CIS MAXIT=200 NZVAR=6 ICHARG=0 MULT=1 $END $SYSTEM TIMLIM=600 MWORDS=1 $END $BASIS NGAUSS=6 GBASIS=N31 NDFUNC=1 DIFFSP=.T. $END $SCF DIRSCF=.T. DAMP=.T. $END $GUESS GUESS=HUCKEL $END $CIS NSTATE=1 $END $STATPT HSSEND=.T. $END $DATA HCHO, S1 state geometry optimization, CIS/6-31+G(d) Cs O C 1 1.205 H 2 1.111 1 121.90 H 2 1.111 1 121.90 3 150.00 $END
これにより、ピラミッド型に構造最適化され、振動計算の結果も虚振動なしで極小化されていることを確認できます。ちなみに、S1(1A”)の構造が実験的に求められていて(Herzberg, G., Electronic spectra and electronic structure of polyatomic molecules, Van Nostrand, New York, 1966)、これと比較すると(Table.2)、定性的には構造は合致していますがC-O結合距離が大きくずれています。このズレは電子相関を取り込むことで修正されます(CASSCF(2,2)/6-31+G(d)による参考値…CASSCFによる構造最適化の一般例は「1重項ビラジカルの構造と遷移状態探索」を参照)。
| r(C-O) (Å) | r(C-H) (Å) | ∠H-C-H (deg) | τ (deg) | |
|---|---|---|---|---|
| exp. | 1.323 | 1.093 | 119 | 31 |
| CIS/6-31G+(d) | 1.2553 | 1.0853 | 118.3 | 24.8 |
| CASSCF(2,2)/6-31+G(d) | 1.3549 | 1.0767 | 118.8 | 39.5 |
表の一番右の列…τは面外角で、もとの平面分子に比べて、H-C-H面がどれくらい面外に傾いているかの値です。
[本稿で行った計算の入出力ファイル( 1.00MB)]
Leave a Reply
コメントを投稿するにはログインしてください。